A tavalyelőtti Astroidea 4k, a Discovery legalapvetőbb eleme a realtime sphere subdiv, vagyis egy gömb részletességének nézőponttól függő, folyamatos változtatása. Az alap algoritmust írom le most.
- Egy ikozaéderből indulunk ki. Ez egy olyan ojjektum, ami 20 háromszögből áll, teljesen mindegy, hogy generálod, csak a vertexek körüljárási sorrendje stimmeljen. Praktikusan a vertexek pozíciója normalizált, vagyis egy egység-gömb felületén ülnek.
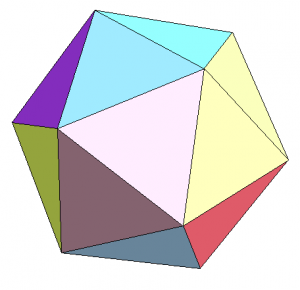
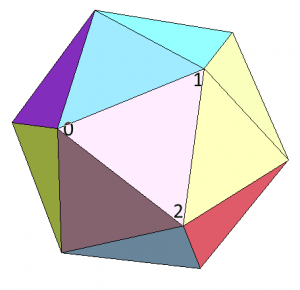
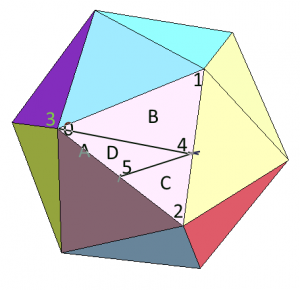
- Húsz háromszöggel indulunk, ez majd a folyamat során változni fog, ez nem befolyásol semmit. A háromszögeken egyesével haladunk, nem teszünk köztük SEMMILYEN különbséget, vagyis az algoritmus nem függ a szomszédos háromszögektől, ami nagyon előnyös tud lenni. Cserébe sajnos indexelést sem nagyon praktikus használni vele, de ez nem egy akkora katasztrófa. Nevezzük el az aktuális háromszög vertexeit 0-1-2-nek.
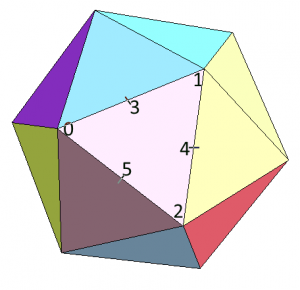
- Fogjuk a háromszög három élét, és generáljunk új vertexeket a felezőpontokra, nevezzük el őket 3-4-5-nek. A poziciókat normalizáljuk, vagyis pld 3=normalize(0+1)
- Az érdekes rész most jön: döntsük el az új vertexekről, hogy szükség van-e rájuk, kell-e ilyen szintű osztás. Fontos, hogy csak az adott él vertexeit használjuk a döntéshez. Pld csinálhatjuk úgy, hogy megnézzük a kamera távolságát az új vertextől, megszorozzuk egy konstanssal (subdiv factor), és az így kapott értéket összehasonlítjuk az eredeti két vertex, vagyis az aktuális él hosszával. Ezzel kapunk egy igen/nem választ, ez még fontos lesz később. Tegyük fel, hogy mindhárom él IGEN-el válaszolt az “osszalak-e tovább” kérdésre, ekkor létrehozhatjuk a négy új háromszöget, amit aztán továbblökünk feldolgozásra. Az eredeti háromszöget el is felejthetjük. (Az új háromszögek: A=0,3,5 B=1,4,3 C=2-5-4 D=3-4-5)
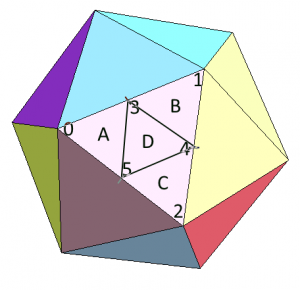
- Tegyük fel, hogy az előző pontban nem minden él adta ugyanazt a választ. Mondjuk a 0-1 él (amin a vertex 3 ül) azt mondta, őt nem kell tovább osztani. Ebben az esetben az adott él felező vertexét (esetünkben a 3-as számút) az él első vertexének (esetünkben a 0-ás számúnak) a pozíciójára állítjuk. Erre nem feltétlenül lenne szükség, hiszen – ahogy majd az ábrán látszik – az egyik háromszög gyakorlatilag eltűnik, de pld hardware megvalósításnál jól jön, hogy MINDIG fix számú háromszöget hozunk létre, maximum némelyik nulla területű. Ha az élek nem értettek egyet, akkor ugyan az eredeti háromszöget elfelejtük, de az újonnan létrehozottak mehetnek azonnal renderelődni, további feldolgozásukra nincs szükség.
- … és így tovább, haladunk a háromszögeken, daraboljuk őket, ha nem kell tovább, akkor rendereljük, ha kell tovább, akkor hozzáadjuk a feldolgozási listához. Előbb-utóbb, ha nem valami végtelen kritériummal dolgozunk, elfogynak a feldolgozandó háromszögek, ezzel kész is vagyunk.
Az élek osztása, illetve az, hogy csak és kizárólag az élek vertexeivel számolunk biztosítja, hogy sosem lesz törés, lyuk, vagy bármi ilyesmi anomália a mesh-en, hiszen két szomszédos háromszög élei matematikailag is ugyanazt a választ fogják adni mindig, bármelyik oldalról nézzük.
Lehetséges még minden háromszögre előszűrést, pld backface vagy frustum szűrést végezni, de óvatosan – egy nagy háromszög nem tökéletes mása a gömb-darabkának, amit reprezentál, pláne, ha később mondjuk displacement is kerül rá (márpedig fog, mert ki akar sima gömböt renderelni:)).

